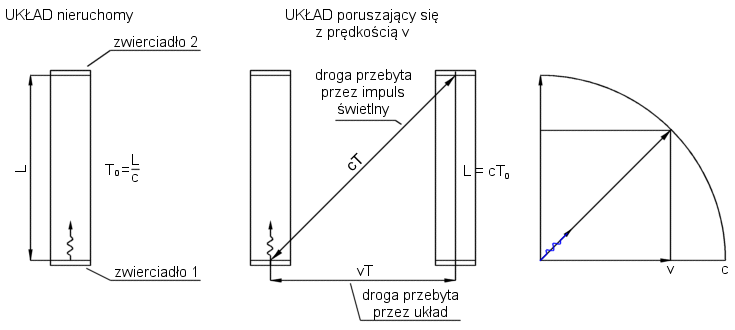
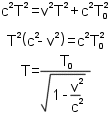Obliczenia do mojego pierścienia do reaktorów fuzji jądrowej - ładunek zgromadzony w połowie pierścienia i średni kąt oddziaływania 45° - średnia wartość fukcji sinus od 0 do 180 stopni wynosi 2 ÷ pi więc oddziaływanie ładunku połowy pierścienia mnożymy przez 2 ÷ pi i porównujemy siłę elektryczną z połowy pierścienia do siły indukcji magnetycznej najsilniejszych magnesów.
Magnes w ITER ma mieć 13 T
Magnesy Wendelstein 7-X 6-15 T
Magnes MIT 20 T
Chińskie magnesy 21,7 - 35,1 T
magnesy Tokamak Energy 24,4 T
Prędkość deuteronu o energii kinetycznej 1 MeV wynosi w przybliżeniu 9,79 × 10⁶ m/s
Maksymalna siła magnetyczna F = q × V × B
Ładunek deuteronu 1,602176634×10^−19 C
Prędkość deuteronu o energii kinetycznej 1 MeV wynosi w przybliżeniu 9,79 × 10⁶ m/s
Indukcja magnetyczna od 6 do 35,1 T
Sprawdzam siłę dla 22 i 35 T
F 22 T = 1,602176634×10^−19 × 9,79 × 10^6 × 22 = 3,45076803 × 10^-11 niutona N
F 35 T = 1,602176634×10^−19 × 9,79 × 10^6 × 35 = 5,48985824 × 10^-11 niutona N
F 35,1 T = 1,602176634×10^−19 × 9,79 × 10^6 × 35,1 = 5,50554355 × 10^-11
Siła pola elektrycznego F = q × E
Natężenia pola elektrycznego pochodzące od połowy naładowanego zjonizowanego pierścienia E = 2 ÷ π × k × Q ÷ r^2 = 2 ÷ π × 1 ÷ ( 4 π × ε₀ ) × Q ÷ r^2
Q ładunek elektryczny połowy naładowanego zjonizowanego pierścienia
Natężenia pola elektrycznego potrzebne do uzyskania ekwiwalentu siły magnetycznej działającej na deuteron o prędkości około 9,79 × 10⁶ m/s w polu magnetycznym 35,1 tesli T
E = F ÷ q
F = 5,50554355 × 10^-11 niutona N
q Ładunek deuteronu 1,602176634×10^−19 C
E = 5,50554355 × 10^-11 ÷ ( 1,602176634×10^−19 ) = 343 629 000,27164 N / C niuton / kulomb
E = 2 ÷ π × 1 ÷ ( 4 π × ε₀ ) × Q ÷ r^2
Q = E × π ÷ 2 × 4 π × ε₀ × r^2 = E × π^2 × 2 × ε₀ × r^2
E = 343 629 000,27164 N / C
ε₀ = 8,854187812813 × 10^−12 F/m
Q = 343 629 000,27164 × π^2 × 2 × 8,854187812813 × 10^−12 × 0,16^2 = 343 629 000,27164 × π^2 × 2 × 8,8541878128 × 10^−12 × 0,16^2 = 0,0015374756 C
Coś mało wyszło jeszcze później na spokojnie to sprawdzę ale jeżeli tu nie ma błędu to wręcz szokująco mało
* edit 2 Dodatkowe sprawdzenie danych
Według analizy poprawności danych przy użyciu ChatGPT i Microsoft Copilot , maksymalna potwierdzona realna gęstość powierzchniowa ładunku / powierzchniowego σ = ~ 10^-3 C / m² , czyli 0,001 C/m² , więc jeżeli limitem jest gęstość powierzchniowa ładunku σ = ~ 0,001 C/m² , to wystarczy zwiększyć powierzchnię metalowych elementów czy metalowej części pierścienia i da się uzyskać obliczony ładunek połowy pierścienia Q = 0,0015374756 C - jeżeli nie da się bardziej naładować pierścienia ładując jego elementy dwustronnie , to przy wymiarach 1 m obwodu - promień około 16 cm , średnica około 32 cm i szerokości pierścienia około 10 - 20 cm czy nawet 30 cm, można zrobić * edit 2 × 6 - 7 - 10 - 20 = 12 - 13 - 14 - 20 - 40 warstwowy pierścień , a jeżeli przy ładowaniu dwustronnym liczy się powierzchnia obu stron , to można zrobić mniej warstw albo zmniejszyć wymiary i można spokojnie uzyskać powierzchnię * edit 2 × 2 m² = 4 m² .


Dla porównania wcześniej obliczyłem że mini kawałek miedzi o wymiarach 1 mm na 1 mm na 1 mm można naładować ładunkiem
Q = 13,5664942388 kulomba C
Przy napięciu jonizacji
U = 33 928 277,445413 V
13,5664942388 C ÷ 0,0015374756 C = 13,5664942388 ÷ 0,0015374756 = 8 823,8761244731 razy mniejszy ładunek więc liczymy ile można zmniejszyć napięcie jonizacji i wymiary kawałka miedzi żeby zachować ładunek 0,0015374756 C
pierwiastek sześcienny cbrt(8 823,8761244731) = 20,6642573027 raza
U = 33 928 277,445413 V ÷ 20,6642573027 = 33 928 277,445413 ÷ 20,6642573027 = 1 641 882,2582595 voltów V
Więc zamiast stosować drogie energochłonne elektromagnesy o indukcji np. 35,1 tesli T wystarczy użyć naładowanego zjonizowanego pierścienia - wystarczy napięcie 1 641 882,2582595 voltów V
Dla porównania małe kieszonkowe paralizatory dostępne w sprzedaży potrafiąc mieć napięcie 50 - 98 milionów voltów V a piorun może mieć napięcie od 100 milionów do 1 miliarda voltów V
5 Litrów miedzi × 8,935 kg/L = 44,675 kg
44,675 kg × 80 zł/kg = 3 574 zł + koszt jonizatora, falownika i innych dodatków
magnes pół mechaniczny elektromechaniczny elektromagnes
Prędkość naelektryzowanych elementów wkomponowanych w obracający się dysk lub pierścień lub walec lub cylinder lub stożek lub kopułę lub sferę lub kulę lub segmentów obracającego się dysku, lub po prostu samego naelektryzowanego dysku np. z przerwą blokującą okrężny przepływ ładunku może wynosić np. 16,67 metrów na sekundę ( m/s ) i to już przy prędkości obrotowej 1000 obrotów na minutę ( obr./min, rpm, rev/min, r/min, r·min−1 ). Dla porównania prędkość dryfu elektronów ( prędkość unoszenia elektronów ) w przewodniku czy prędkość super- / nad- prądu w nadprzewodniku mieści się w granicach od 0,1 do 1 milimetra na sekundę. Do tego zamiast zwiększać procentowe naładowanie elementów dysku czy samego dysku można zwiększyć ilość poruszającego się ładunku przez zwiększenie objętości naładowanych elementów dysku czy samego dysku.

magnes pół mechaniczny elektromechaniczny elektromagnes
Najsilniejszy magnes na świecie najsilniejszy elektromagnes na świecie magnes pół mechaniczny elektromechaniczny elektromagnes elektro mechaniczny najpotężniejszy na świecie
Koncept elektromechanicznego elektromagnesu o niższym zużyciu energii i większej sile niż powszechnie znane magnesy, który może umożliwić budowę tańszych reaktorów fuzji jądrowej wodoru, budowę statków kosmicznych o większym zasięgu, umożliwić lewitację większych zwierząt niż w magnesach Bittera oraz umożliwić budowę łodzi, statków i desek lewitujących nad wodą przy niższym zużyciu energii. Elektromechaniczny elektromagnes ( półmechaniczny elektromagnes ) to rodzaj magnesu, w którym pole magnetyczne wytwarzane jest przez obracający się pierścień lub np. dysk z wkomponowanymi naładowanymi elementami i np. przy prędkości obrotowej 1000 obr./min zapewnia on prędkość elektronów lub dodatnich jonów wynoszącą np. 16,67 m/s przy średnicy około 32 cm / 12,6 cala.
Dla porównania, prędkość dryfu elektronów ( prędkość unoszenia elektronów ) w przewodniku lub prędkość superprądu w nadprzewodniku waha się w granicach od 0,1 do 1 milimetra na sekundę.
Ponadto, zamiast zwiększać procentowy ładunek elementów pierścienia lub dysku, można zwiększyć ilość poruszającego się ładunku poprzez zwiększenie objętości naładowanych elementów pierścienia lub dysku.
* edit Dorzucam obliczenia
Wzór na prędkość dryfu elektronów w przewodniku u=I/nAe zatem ekwiwalent prądu I=unAe
u - prędkości dryfu elektronów lub jonów dodatnich wirującego naładowanego pierścienia lub dysku = 2πr × obr. / min / 60
n - liczba elektronów na metr sześcienny = stała Avogadra × liczba moli na metr sześcienny × liczba zjonizowanych elektronów walencyjnych
np. dla miedzi np. przy jonizacji 1 elektronu na każdy atom liczba zjonizowanych elektronów n na metr sześcienny = 6,02214076×10^23 mol^-1 × 140 606,80451956 mol/m^3 × 1 = 8,46753969×10^28 m^-3
A - przekrój poprzeczny
np. dla pierścienia lub dysku o średnicy około 32 cm, czyli promieniu 0,16 m - obwód około 1 metra i np. 5 Litrów miedzi = 0,005 m^3 miedzi = 0,005 m^3 / około 1 metr = około 0,005 m^2
Grubość takiego pierścienia √(0,005 m^2) = 0,0707 m, czyli 7,07 cm
e - ładunek elementarny elektronu = -1,602176634×10^−19 C
I - ekwiwalent prądu = unAe = 16,67 m/s × 8,46753969×10^28 m^-3 × 0,005 m^2 × 1,602176634×10^−19 C = 16,67 × 8,46753969×10^28 × 0,005 × 1,602176634×10^−19 = 1 130 767 294,8028 amperów
dla porównania prąd w elektromagnesie Bittera o indukcji magnetycznej 16 tesli podczas pracy wynosi około 20 000 amperów
1 000 000 000 amperów / 20 000 amperów = 50 000 razy większy ekwiwalent prądu niż prąd w magnesie 16 tesli Bittera z tym że w magnesach Bittera może być około 1000 talerzy przewodzących prąd, więc przy 1 wirującym naładowanym pierścieniu lub dysku o podanych wcześniej wymiarach 7,07 × 7,07 cm i obwodzie 1 m różnica prądu wynosi około 50 razy oprócz tego z jednej strony pierścień 7 cm jest jednak około 4-8 razy cieńszy od stosu 1000 talerzy i to zwiększa gęstość pola magnetycznego a z drugiej strony otwór w środku pierścienia lub dysku ma np. około 60 razy większą powierzchnię niż w elektromagnesie Bittera i to z kolei zmniejsza gęstość pola magnetycznego
50 × 16 tesli = 800 tesli T
800 tesli ÷ 7,5 lub 15 = 106,67 lub 53,33 tesli T
jednak ze względu na przeciwny ruch ładunków po lewej i prawej stronie pierścienia lub dysku siły magnetyczne rozrywają pierścień lub dysk, oprócz tego siły magnetyczne ściskają pierścień lub dysk w kierunku równoległym do jego osi i trzeba się limitować np. do 80 tesli T żeby nie uszkodzić dysku.
W próbach niszczących pierścień lub dysk można go rozkręcić do prędkości ponad 100 000 - 300 000 obr. / min i teoretycznie uzyskać indukcję magnetyczną ponad 80 000 - 240 000 tesli T ÷ 7,5 lub 15 = 5 333,33 - 32 000 tesli T
obliczenia napięcia potrzebnego do jonizacji metalowego pierścienia lub dysku np. z miedzi
Na podstawie gęstości miedzi według popularnej wersji 8935 kg/m^3, masy molowej atomowej miedzi 63,546 g/mol i stałej Avogadra 6,02214076×10^23 mol^−1 obliczam najpierw ilość atomów miedzi na metr sześcienny i grubość 1 atomu w bloku miedzi 8935000 g/m3 ÷ 63,546 g/mol = 140 606,80451956 mol/m^3
140 606,80451956 mol/m^3 × 6,02214076×10^23 mol^−1 = 8,46753969 × 10^28 atomów / m^3
Pierwiastek sześcienny cbrt(8,46753969×10^28) = 4 391 225 573,3491 atomów / m
Grubość 1 atomu w bloku miedzi = 1 m ÷ 4 391 225 573,3491 atomów/m = 0,227726857 × 10^-9 m czyli nano metra
Przy 1 styku podłączenia do jonizatora po przeciwnej stronie względem przerwy w pierścieniu
napięcie jonizujące ma do pokonania szereg atomów o grubości 0,5 m
0,5 m × 4 391 225 573,3491 atomów/m = 2 195 612 786,6746 atomów od miejsca podłączenia jonizatora do przerwy w dysku
Na podstawie energii jonizacji zakładam napięcie jonizacji 1 atomu miedzi 7,72638 V można też sprawdzić napiecia 4,53 - 5,10 V na podstawie pracy wyjścia / funkcji pracy
7,72638 V × 2 195 612 786,6746 atomów = 16 964 138 722,707 V
więc dysk trzeba podzielić wzdłuż obwodu na co najmniej 100 lub lepiej 200 części, grubość i szerokość na 14,14 lub 28,28 części, czyli na co najmniej 100 - 200 × 14,14 × 14,14 = 19 993,96 - 39 987,92 części lub lepiej 200 - 400 × 28,28 × 28,28 = 159 951,68 - 319 903,36 części żeby zejść z napięciem jonizacji z 16,96 miliardów voltów V do chociaż 169,64 milionów voltów V lub np. 84,82 milionów voltów V
Dla porównania małe kieszonkowe paralizatory dostępne w sprzedaży potrafiąc mieć napięcie 50 - 98 milionów voltów V a piorun może mieć napięcie od 100 milionów do 1 miliarda voltów V
5 Litrów miedzi × 8,935 kg/L = 44,675 kg
44,675 kg × 80 zł/kg = 3 574 zł + koszt jonizatora, falownika i innych dodatków
Obliczenia
Q - ładunek ekektryczny = liczba dodanych lub odjętych elektronów elektronów / m^3 × objętość x ładunek elementarny elektronu =
8,46753969×10^28 m^-3 × 0,000000001 m^3 × 1,602176634×10^−19 C = 8,46753969×10^28 × 0,000000001 × 1,602176634×10^−19 = 13,5664942388 kulomba C
Długość boku kawałka bloku miedzi = Pierwiastek sześcienny z 0,000000001 m^3 = cbrt(0,000000001) = 0,001 m czyli 1 mili metr mm
0,001 m × 4 391 225 573,3491 atomów/m = 4 391 225,5733491 atomów
Na podstawie energii jonizacji zakładam napięcie jonizacji 1 atomu miedzi 7,72638 V można też sprawdzić napiecia 4,53 - 5,10 V na podstawie pracy wyjścia / funkcji pracy
4 391 225,5733491 atomów × 7,72638 V = 33 928 277,445413 V
13,5664942388 C × 33 928 277,445413 V = 13,5664942388 × 33 928 277,445413 = 460 287 780,4956 dżulów J
Akumulator o pojemności 100 kWh ma 360 000 000 dżulów J
460 287 780,4956 J ÷ 360 000 000 J = 460 287 780,4956 ÷ 360 000 000 = 1,278577168 razy większa / wyższa pojemność więc liczymy ile można zmniejszyć napięcie jonizacji i wymiary kawałka miedzi żeby zachować 100 kWh pojemności √(√(1,278577168)) = 1,0633634685 raza
33 928 277,445413 V ÷ 1,0633634685 = 31 906 566,710697 voltów V zatem Kawałek bryła miedzi mniejsza niż 0,000001 litrów czyli 0,000001 × 8,935 kg/L = 0,000008935 kg = 0,008935 g lub wiele mniejszych kawałków miedzi może kiedyś zastąpić inne akumulatory już przy napięciach 31 906 566,710697 voltów V
Bryła 5 Litrów miedzi jako akumulator
Obliczenia
Q - ładunek ekektryczny = liczba dodanych lub odjętych elektronów elektronów / m^3 × objętość x ładunek elementarny elektronu =
8,46753969×10^28 m^-3 × 0,005 m^3 × 1,602176634×10^−19 C = 8,46753969×10^28 × 0,005 × 1,602176634×10^−19 = 67 832 471,193928 C
Długość boku bloku miedzi = Pierwiastek sześcienny z 0,005 m^3 = cbrt(0,005) = 0,1709975947 m
0,1709975947 m × 4 391 225 573,3491 atomów/m = 750 889 010,82782 atomów
750 889 010,82782 atomów × 7,72638 V = 5 801 653 835,4799 V
67 832 471,193928 C × 5 801 653 835,4799 V = 67 832 471,193928 × 5 801 653 835,4799 = 3,93540517 × 10^17 J
Akumulator o pojemności 100 kWh ma 360 000 000 dżulów J
3,93540517 × 10^17 J ÷ 360 000 000 J = 3,93540517 × 10^17 ÷ 360 000 000 = 1 093 168 102,7778 razy większa / wyższa pojemność więc liczymy ile można zmniejszyć napięcie jonizacji i wymiary kawałka miedzi żeby zachować 100 kWh pojemności √(√(1 093 168 102,7778)) = 181,8325954245 razy
5 801 653 835,4799 V ÷ 181,8325954245 = 31 906 566,707336 voltów V zatem bryła miedzi 6 011 947,9690954 razy mniejsza niż 5 litrów czyli 5 ÷ 6 011 947,9690954 × 8,935 kg/L = 0,000007431 kg = 0,007431 g lub wiele mniejszych kawałków miedzi może kiedyś zastąpić inne akumulatory już napięciach 31 906 566,710697 voltów V
Obliczenia dla napięcia akumulatora 1000, 2000, 3000, 4000, 5000, ... voltów V
1000 V / 7,72638 V = 129,4267172984 atomów
129,4267172984 atomów × grubość 1 atomu w bloku miedzi 0,227726857 × 10^-9 m = 29,4739395×10^-9 m czyli około 30 nano metrów
(29,4739395×10^-9)^3 × 8,46753969×10^28 m^-3 = 2 168 062,5322705 atomów i elektronów w sześcianie o boku 30 nano metrów
Ładunek = 2 168 062,5322705 × 1,602176634×10^−19 = 3,47361913×10^-13 kulomba C
Pojemność = Ładunek × napięcie
3,47361913×10^-13 × 1000 = 3,47361913×10^-10 dżula J
Akumulator o pojemności 100 kWh ma 360 000 000 dżulów J
360 000 000 ÷ (3,47361913×10^-10) = 1,03638305×10^18 czyli trylion nano kawałków miedzi
2000 V ÷ 7,72638 V = 258,8534345968 atomów
258,8534345968 atomów × grubość 1 atomu w bloku miedzi 0,227726857 × 10^-9 m = 58,9478791×10^-9 m czyli około 59 nano metrów
(58,9478791×10^-9)^3 × 8,46753969×10^28 m^-3 = 17 344 500,346435 atomów i elektronów w sześcianie o boku 58,9 nano metra
Ładunek = 17 344 500,346435 × 1,602176634×10^−19 = 2,77889532×10^-12 kulomba C
Pojemność = Ładunek × napięcie
2,77889532×10^-12 × 2000 = 5,55779064×10^-9 dżula J
Akumulator o pojemności 100 kWh ma 360 000 000 dżulów J
360 000 000 ÷ (5,55779064×10^-9) = 6,47739405×10^16 czyli około 65 biliardów nano kawałków miedzi
1 grosz za mniej niż 1 gram miedzi + koszt jonizatora, falownika i innych dodatków
To jest liczone dla wyładowania do ziemi - jeżeli nie da się wykonać wyładowania do ziemi to trzeba podzielić ten kawałek bryłę na 2 części lub dodać drugi kawałek bryłę
3000 V ÷ 7,72638 V = 388,2801518952 atomów
388,2801518952 atomów × grubość 1 atomu w bloku miedzi 0,227726857 × 10^-9 m = 88,4218186×10^-9 m czyli około 88,4 nano metra
(88,4218186×10^-9)^3 × 8,46753969×10^28 m^-3 = 58 537 688,569913 atomów i elektronów w sześcianie o boku 88,4 nano metra
Ładunek = 58 537 688,569913 × 1,602176634×10^−19 = 9,37877168×10^-12 kulomba C
Pojemność = Ładunek × napięcie
9,37877168×10^-12 × 3000 = 2,81363150×10^-8 dżula J
Akumulator o pojemności 100 kWh ma 360 000 000 dżulów J
360 000 000 ÷ (2,81363150×10^-8) = 1,27948525×10^16 czyli około 12,8 biliardów nano kawałków miedzi
4000 V ÷ 7,72638 V = 517,7068691936 atomów
517,7068691936 atomów × grubość 1 atomu w bloku miedzi 0,227726857 × 10^-9 m = 117,895758×10^-9 m czyli około 117,9 nano metra
(117,895758×10^-9)^3 × 8,46753969×10^28 m^-3 = 138 756 002,06531 atomów i elektronów w sześcianie o boku 117,9 nano metra
Ładunek = 138 756 002,06531 × 1,602176634×10^−19 = 22,2311624×10^-12 kulomba C
Pojemność = Ładunek × napięcie
22,2311624×10^-12 × 4000 = 8,89246496×10^-8 dżula J
Akumulator o pojemności 100 kWh ma 360 000 000 dżulów J
360 000 000 ÷ (8,89246496×10^-8) = 4,04837131×10^15 czyli około 4 biliardów nano kawałków miedzi
5 Litrów miedzi × 8,935 kg/L = 44,675 kg
44,675 kg × 80 zł/kg = 3 574 zł + koszt jonizatora, falownika i innych dodatków
Promieniowanie pochodzące od przyspieszanego ładunku
Zmienne pole magnetyczne, promieniowanie elektromagnetyczne, indukcja elektromagnetyczna
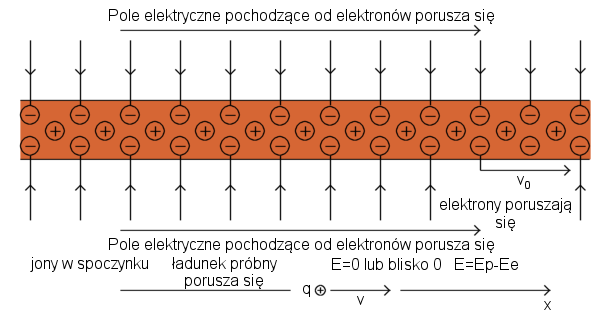
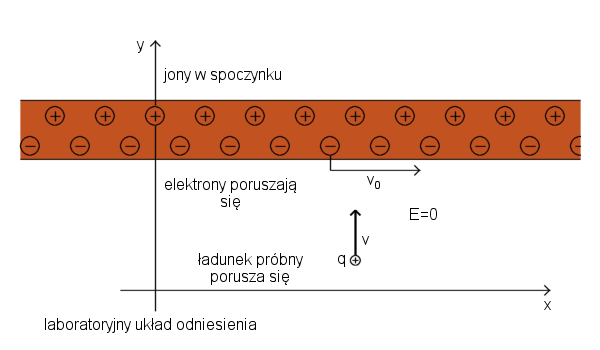
Pole elektryczne porusza się z prędkością, którą miała cząstka podczas emisji tego pola.


Pole elektryczne ładunku, który się zatrzymuje
Załóżmy, że ładunek q poruszał się ze stałą prędkością v0 w kierunku x przez dłuższy czas. Nagle zatrzymuje się po krótkim okresie stałego hamowania. Pole elektryczne ładunku rozchodzi się radialnie na zewnątrz i porusza się z prędkością, którą miał ładunek podczas emisji tego pola.
Wykres zależności prędkości od czasu

Pole elektryczne
Zakładając, że v0 ≪ c możemy zaniedbać relatywistyczną kompresję linii pola. Czas t=0 to była chwila, gdy rozpoczęło się hamowanie, a położenie x=0 to położenie cząstki w tamtej chwili. Cząstka przemieściła się trochę dalej przed zatrzymaniem, Δx=1/2*v0Δt1. Ten dystans jest bardzo mały w porównaniu z innymi odległościami na rysunku.
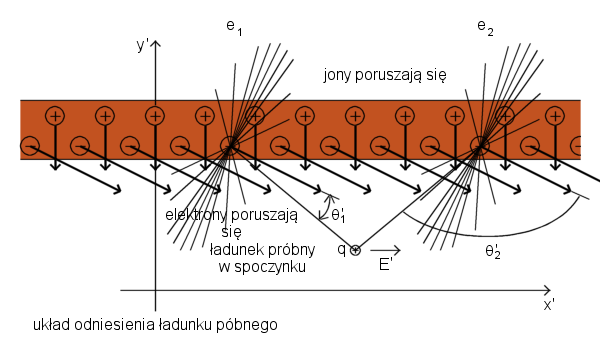
Teraz przyjrzyjmy się polu elektrycznemu w chwili t=Δt2≫Δt1. Pole elektryczne osiąga dystans R=cΔt2. Zatem, pole w obszarze I musi być polem ładunku, który się poruszał i nadal się porusza ze stałą prędkością v0. Wydaje się, że to pole pochodzi z punktu x=v0Δt2 na osi x. To jest tam, gdzie cząstka byłaby teraz, gdyby się nie zatrzymała. Z drugiej strony, pole w odległości mniejszej niż c(Δt2-Δt1), w obszarze II musi być polem cząstki w spoczynku blisko pozycji x=0 (dokładnie w x=1/2*v0Δt1).

Jakie musi być pole w obszarze przejściowym, sferycznej powłoce o grubości cΔt1 pomiędzy obszarem I i obszarem II? Odcinek linii pola AB leży na stożku w okół osi x, który zawiera pewną ilość strumienia pochodzącego od ładunku q. Ze względu na prawo Gaussa, jeżeli CD tworzy ten sam kąt θ z osią, stożek, na którym on leży zawiera taką samą ilość strumienia. (Ze względu na to, że v0 ≪ c, możemy zaniedbać relatywistyczną kompresję linii pola.) Dlatego AB i CD muszą być częściami tej samej linii pola, połączonej przez odcinek BC. Odcinek linii BC pokazuje nam kierunek pola E wewnątrz powłoki. To pole E wewnątrz powłoki ma zarówno składową radialną Er, jak i składową poprzeczną Eθ. Z geometrii rysunku ich stosunek jest łatwo znaleźć.

(1)
Ze względu na prawo Gaussa, E
r musi mieć taką samą wartość wewnątrz grubości powłoki, jaką ma w obszarze II blisko B. Dlatego E
r=q/4πε
0R
2=q/4πε
0c
2Δt
22, i stosując to w Równaniu. 1 otrzymujemy

(2)
I v
0/Δt
1 = a, wartość (negatywnego) przyspieszenia, a cΔt
2= R, więc nasz rezultat może być zapisany w postaci

(3)
Objawił się tutaj niezwykły fakt: E
θ jest proporcjoalne do 1/R, nie do 1/R
2! W miarę upływu czasu i wraz ze wzrostem R poprzeczne pole E
θ ostatecznie stanie się dużo silniejsze niż E
r. Towarzyszyć temu poprzecznemu polu elektrycznemu (,które jest prostopadłe do R) będzie pole magnetyczne o równej sile poprzecznej do zarówno R, jak i E. To jest ogólna własność fali elektromagnetycznej.
Teraz obliczamy energię zgromadzoną w poprzecznym polu elektrycznym powyżej, w całej sferycznej powłoce. Gęstość energii równa się

(4)
Objętość powłoki równa się 4πR
2cΔt
1, a średnia wartość sin
2θ po powierzchni kuli równa się 2/3. Całkowita energia poprzecznego pola elektrycznego równa się zatem

(5)
Do tego musimy dodać równą ilość dla energii zgromadzonej w poprzecznym polu magnetycznym:
Całkowita energia w poprzecznym polu elektromagnetycznym równa się

(6)
Promień R zniósł się. Ta ilość energii poprostu rozchodzi się na zewnątrz, niesłabnąca, z prędkością c od strony hamowania. Ze względu na to, że Δt
1 jest czasem hamowania i jest także czasem impulsu
elektromagnetycznego, który mierzy odległy obserwator, możemy powiedzieć, że moc promieniowana podczas procesu przyspieszania równała się

(7)
Jako, że jest to kwadrat chwilowego przyspieszenia, które pojawia się w Równaniu 7, nie ma znaczenia czy a jest dodatnie czy ujemne. Oczywiście nie powinno, dla zatrzymywania w jednym układzie inercjalnym może być
startowaniem w innym. Mówiąc o róznych układach, P
rad samo okazuje się być niezmiennicze względem transformacji Lorentza, co jest czasem bardzo przydatne. To dlatego, że P
rad to
energia/czas, a energia trasformuje się tak jak czas, zawsze będąc czwartą składową czterowektora. Mamy tutaj bardziej ogólny rezultat niż mogliśmy się spodziewać. Równanie 7 prawidłowo daje chwilową ilość
promieniowania energii przez naładowaną cząstkę poruszającą się ze zmiennym przyspieszeniem-na przykład, cząstkę poruszającą się ruchem harmonicznym prostym. Odnosi się to do szerokiej gamy systemów
promieniujących od anten radiowych do atomów i jąder.
Radiating Charge simulation - PhET INTERACTIVE SIMULATIONS
Purcell appendix B in the CGS system




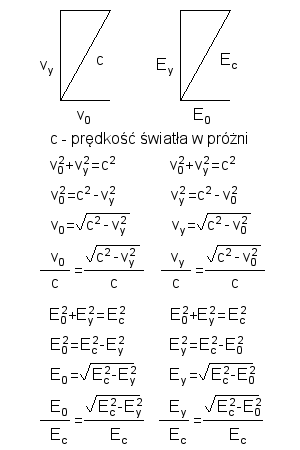








 (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7)